Первичном рынке критерий фишера. Критерий фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей - документ

Критерий Фишера

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону. Он является параметрическим критерием.

F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий.

Пусть в результате наблюдений получены две выборки. По ним вычислены дисперсии и , имеющие и степеней свободы. Будем считать, что первая выборка взята из генеральной совокупности с дисперсией , а вторая – из генеральной совокупности с дисперсией . Выдвигается нулевая гипотеза о равенстве двух дисперсий, т.е. H 0:
или . Для того, чтобы отвергнуть эту гипотезу нужно доказать значимость различия при заданном уровне значимости
.

Значение критерия вычисляется по формуле:

Очевидно, что при равенстве дисперсий величина критерия будет равна единице. В остальных случаях она будет больше (меньше) единицы.

Критерий имеет распределение Фишера
. Критерий Фишера – двусторонний критерий, и нулевая гипотеза
отвергается в пользу альтернативной
если . Здесь , где
– объем первой и второй выборки соответственно.

В системе STATISTICA реализован односторонний критерий Фишера, т.е. в качестве всегда берут максимальную дисперсию. В этом случае нулевая гипотеза отвергается в пользу альтернативы , если .

Пример

Пусть поставлена задача, сравнить эффективность обучения двух групп студентов. Уровень успеваемости - характеризует уровень управления процессом обучения, а дисперсия качество управления обучением, степень организованности процесса обучения. Оба показателя являются независимыми и в общем случае должны рассматриваться совместно. Уровень успеваемости (математическое ожидание) каждой группы студентов характеризуется средними арифметическими и , а качество характеризуется соответствующими выборочными дисперсиями оценок: и . При оценке уровня текущей успеваемости оказалось, что он одинаков у обоих учащихся: = = 4,0. Выборочные дисперсии:
и
. Числа степеней свободы, соответствующие этим оценкам:
и
. Отсюда для установления различий в эффективности обучения мы можем воспользоваться стабильностью успеваемости, т.е. проверим гипотезу .

Вычислим
(в числителе должна быть большая дисперсия), . По таблицам (STATISTICA – Probability Distribution Calculator ) находим , которое меньше вычисленного, следовательно нулевая гипотеза должна быть отвергнута в пользу альтернативы . Это заключение может не удовлетворить исследователя, поскольку его интересует истинная величина отношения
(у нас в числителе всегда большая дисперсия). При проверке одностороннего критерия получим , что меньше вычисленного выше значения. Итак, нулевая гипотеза должна быть отвергнута в пользу альтернативы .

Критерий Фишера в программе STATISTICA в среде Windows

Для примера проверки гипотезы (критерий Фишера) используем (создаем) файл с двумя переменными (fisher.sta):

Рис. 1. Таблица с двумя независимыми переменными

Чтобы проверить гипотезу необходимо в базовой статистике (Basic Statistics and Tables ) выбрать проверку по Стьюденту для независимых переменных. (t-test, independent, by variables ).

Рис. 2. Проверка параметрических гипотез

После выбора переменных и нажатия на клавишу Summary производится подсчет значений среднеквадратичных отклонений и критерия Фишера. Кроме этого определяется уровень значимости p , при котором различие несущественно.

Рис. 3. Результаты проверки гипотезы (F- критерий)

Используя Probability Calculator и задав значение параметров можно построить график распределения Фишера с пометкой вычисленного значения.

Рис. 4. Область принятия (отклонения) гипотезы (F- критерий)

Источники.

Проверка гипотез об отношениях двух дисперсий

URL: /tryphonov3/terms3/testdi.htm

Лекция 6. :8080/resources/math/mop/lections/lection_6.htm

F – критерий Фишера

URL: /home/portal/applications/Multivariatadvisor/F-Fisheer/F-Fisheer.htm

Теория и практика вероятностно-статистических исследований.

URL: /active/referats/read/doc-3663-1.html

F – критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух независимых выборок. Для вычисления F эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фи­шера такова:

где - дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F эмп всегда будет больше или равно единице.

Чис­ло степеней свободы определяется также просто:

k 1 =n l - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k 2 = n 2 - 1 для второй выборки.

В Приложе­нии 1 критические значения критерия Фишера находятся по величинам k 1 (верхняя строчка таблицы) и k 2 (левый столбец таблицы).

Если t эмп >t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос - есть ли различия в степени однородности показателей умственного развития между классами.

Решение. Для критерия Фишера необходимо сравнить дис­персии тестовых оценок в обоих классах. Резуль­таты тестирования представлены в таблице:

Таблица 3.

№№ учащихся	Первый класс	Второй класс

Рассчитав дисперсии для переменных X и Y, получаем:

s x 2 =572,83; s y 2 =174,04

Тогда по формуле (8) для расчета по F критерию Фишера находим:

По таблице из Приложения 1 для F критерия при степенях свободы в обоих случаях равных k=10 - 1 = 9 находим F крит =3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Непараметрические критерии

Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.

)

Расчет критерия φ*

1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого "есть эффект" и тех, у кого "нет эффекта". Если признак измерен количественно, использовать критерий λ для поиска опти­мальной точки разделения.

2. Начертить четырёхклеточную (синоним: четырёхпольная) таблицу из двух столбцов и двух строк. Пер­вый столбец - "есть эффект"; второй столбец - "нет эффекта"; первая стро­ка сверху - 1 группа (выборка); вторая строка - 2 группа (выборка).

4. Подсчитать количество испытуемых в первой выборке, у которых "нет эф­фекта", и занести это число в правую верхнюю ячейку таблицы. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством ис­пытуемых в первой группе.

6. Подсчитать количество испытуемых во второй выборке, у которых "нет эф­фекта", и занести это число в правую нижнюю ячейку таблицы. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством ис­пытуемых во второй группе (выборке).

7. Определить процентные доли испытуемых, у которых "есть эффект", путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.

8. Проверить, не равняется ли одна из сопоставляемых процентных долей ну­лю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно или нежелательно, от­казаться от критерия φ* и использовать критерий χ2.

9. Определить по Табл. XII Приложения 1 величины углов φ для каждой из сопоставляемых процентных долей.

где: φ1 - угол, соответствующий большей процентной доле;

φ2 - угол, соответствующий меньшей процентной доле;

N1 - количество наблюдений в выборке 1;

N2 - количество наблюдений в выборке 2.

11. Сопоставить полученное значение φ* с критическими значениями: φ* ≤1,64 (р<0,05) и φ* ≤2,31 (р<0,01).

Если φ*эмп ≤φ*кр. H0 отвергается.

При необходимости определить точный уровень значимости полученного φ*эмп по Табл. XIII Приложения 1.

Данный метод описан во многих руководствах (Плохинский Н.А., 1970; Гублер Е.В., 1978; Ивантер Э.В., Коросов А.В., 1992 и др.) Настоящее описание опирается на тот вариант метода, который был разработан и изложен Е.В. Гублером.

Назначение критерия φ*

Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта (показателя). Чем он больше, тем достовернее различия.

Описание критерия

Критерий оценивает достоверность различий между теми процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект (показатель). Образно говоря, мы сравниваем между собой 2 лучших куска, вырезанные из 2-х пирогов, и решаем, какой из них действительно больше.

Суть углового преобразования Фишера состоит в переводе процент­ных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол ф, а меньшей доле - меньший угол, но соотношения здесь не линейные:

где Р - процентная доля, выраженная в долях единицы (см. Рис. 5.1).

При увеличении расхождения между углами φ 1 и φ 2 и увеличе­ния численности выборок значение критерия возрастает. Чем больше величина φ* , тем более вероятно, что различия достоверны.

Гипотезы

H 0 : Доля лиц , у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.

H 1 : Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.

Графическое представление критерия φ*

Метод углового преобразования несколько более абстрактен, чем остальные критерии.

Формула, которой придерживается Е. В. Гублер при подсчете значений φ, предполагает, что 100% составляют угол φ=3,142, то есть округленную величину π=3,14159... Это позволяет нам представить со­поставляемые выборки в виде двух полукругов, каждый из которых символизирует 100% численности своей выборки. Процентные доли испытуемых с "эффектом" будут представлены как секторы, образован­ные центральными углами φ. На Рис. 5.2 представлены два полукруга, иллюстрирующие Пример 1. В первой выборке 60% испытуемых ре­шили задачу. Этой процентной доле соответствует угол φ=1,772. Во второй выборке 40% испытуемых решили задачу. Этой процентной доле соответствует угол φ =1,369.

Критерий φ* позволяет определить, действительно ли один из углов статистически достоверно превосходит другой при данных объе­мах выборок.

Ограничения критерия φ*

1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным (Гублер Е.В., 1978, с. 86).

2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими.

Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:

а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:

б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:

в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:

г) при n 1 , n 2 ≥ 5 возможны любые сопоставления.

В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n 1 =2, n 2 = 15, но в этих слу­чаях не удастся выявить достоверных различий.

Других ограничений у критерия φ* нет.

Рассмотрим несколько примеров, иллюстрирующих возможности критерия φ*.

Пример 1: сопоставление выборок по качественно определяемому при­знаку.

Пример 2: сопоставление выборок по количественно измеряемому при­знаку.

Пример 3: сопоставление выборок и по уровню, и по распределению признака.

Пример 4: использование критерия φ* в сочетании с критерием X Колмогорова-Смирнова в целях достижения максимально точного результата.

Пример 1 - сопоставление выборок по качественно определяемому признаку

В данном варианте использования критерия мы сравниваем про­цент испытуемых в одной выборке, характеризующихся каким-либо ка­чеством, с процентом испытуемых в другой выборке, характеризующих­ся тем же качеством.

Допустим, нас интересует, различаются ли две группы студентов по успешности решения новой экспериментальной задачи. В первой группе из 20 человек с нею справились 12 человек, а во второй выбор­ке из 25 человек - 10. В первом случае процентная доля решивших за­дачу составит 12/20·100%=60%, а во второй 10/25·100%=40%. Дос­товерно ли различаются эти процентные доли при данных n 1 и n 2 ?

Казалось бы, и "на глаз" можно определить, что 60% значи­тельно выше 40%. Однако на самом деле эти различия при данных n 1 , n 2 недостоверны.

Проверим это. Поскольку нас интересует факт решения задачи, будем считать "эффектом" успех в решении экспериментальной задачи, а отсутствием эффекта - неудачу в ее решении.

Сформулируем гипотезы.

H 0 : Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.

H 1 : Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе.

Теперь построим так называемую четырехклеточную, или четы­рехпольную таблицу, которая фактически представляет собой таблицу эмпирических частот по двум значениям признака: "есть эффект" - "нет эффекта".

Таблица 5.1

Четырехклеточная таблица для расчета критерия при сопоставлении двух групп испытуемых по процентной доле решивших задачу.

Группы	"Есть эффект": задача решена			"Нет эффекта": задача не решена			Суммы
	Количество испытуемых	% доля		Количество испытуемых	% доля
1 группа		(60%)			(40%)
2 группа		(40%)			(60%)
Суммы

В четырехклеточной таблице, как правило, сверху размечаются столбцы "Есть эффект" и "Нет эффекта", а слева - строки "1 группа" и "2 группа". Участвуют в сопоставлениях, собственно, только поля (ячейки) А и В, то есть процентные доли по столбцу "Есть эффект".

По Табл. XII Приложения 1 определяем величины φ, соответст­вующие процентным долям в каждой из групп.

Теперь подсчитаем эмпирическое значение φ* по формуле:

где φ 1 - угол, соответствующий большей % доле;

φ 2 - угол, соответствующий меньшей % доле;

n 1 - количество наблюдений в выборке 1;

n 2 - количество наблюдений в выборке 2.

В данном случае:

По Табл. XIII Приложения 1 определяем, какому уровню значи­мости соответствует φ* эмп =1,34:

р=0,09

Можно установить и критические значения φ*, соответствующие принятым в психологии уровням статистической значимости:

Построим "ось значимости".

Полученное эмпирическое значение φ* находится в зоне незна­чимости.

Ответ: H 0 принимается. Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.

Можно лишь посочувствовать исследователю, который считает существенными различия в 20% и даже в 10%, не проверив их досто­верность с помощью критерия φ*. В данном случае, например, досто­верными были бы только различия не менее чем в 24,3%.

Похоже, что при сопоставлении двух выборок по какому-либо качественному признаку критерий φ может нас скорее огорчить, чем обрадовать. То, что казалось существенным, со статистической точки зрения может таковым не оказаться.

Гораздо больше возможностей порадовать исследователя появля­ется у критерия Фишера тогда, когда мы сопоставляем две выборки по количественно измеренным признакам и можем варьировать "эффект.

Пример 2 - сопоставление двух выборок по количественно изме­ряемому признаку

В данном варианте использования критерия мы сравниваем про­цент испытуемых в одной выборке, которые достигают определенного уровня значения признака, с процентом испытуемых, достигающих этого уровня в другой выборке.

В исследовании Г. А. Тлегеновой (1990) из 70 юношей - уча­щихся ПТУ в возрасте от 14 до 16 лет было отобрано по результатам обследования по Фрайбургскому личностному опроснику 10 испытуемых с высоким показателем по шкале Агрессивности и 11 испытуемых с низким показателем по шкале Агрессивности. Необходимо определить, различаются ли группы агрессивных и неагрессивных юношей по пока­зателю расстояния, которое они спонтанно выбирают в разговоре с со­курсником. Данные Г. А. Тлегеновой представлены в Табл. 5.2. Мож­но заметить, что агрессивные юноши чаще выбирают расстояние в 50 см или даже меньше, в то время как неагрессивные юноши чаще выби­рают расстояние, превышающее 50 см.

Теперь мы можем рассматривать расстояние в 50 см как крити­ческое и считать, что если выбранное испытуемым расстояние меньше или равно 50 см, то "эффект есть", а если выбранное расстояние боль­ше 50 см, то "эффекта нет". Мы видим, что в группе агрессивных юношей эффект наблюдается в 7 из 10, т. е. в 70% случаев, а в группе неагрессивных юношей - в 2 из 11, т. е. в 18,2% случаев. Эти про­центные доли можно сопоставить по методу φ* , чтобы установить дос­товерность различий между ними.

Таблица 5.2

Показатели расстояния (в см), выбираемого агрессивными и неагрессивными юношами в разговоре с сокурсником (по данным Г.А. Тлегеновой, 1990)

	Группа 1: юноши с высокими показателями по шкале Агрессивности FPI - R (n 1 =10)		Группа 2: юноши с низкими значениями по шкале Агрессивности FPI - R (n 2 =11)
	d(c м )	% доля	d(c M )	% доля
"Есть эффект" d ≤50 см
				18,2%
"Нет эффекта" d>50 см
	80 QO			81,8%
Суммы		100%		100%
Средние	5б:о		77.3

Сформулируем гипотезы.

H 0 d ≤ 50 см, в группе агрес­сивных юношей не больше, чем в группе неагрессивных юношей.

H 1 : Доля лиц, которые выбирают дистанцию d ≤ 50 см, в группе агрес­сивных юношей больше, чем в группе неагрессивных юношей. Теперь построим так называемую четырехклеточную таблицу.

Таблица 53

Четырехклеточная таблица для расчета критерия φ* при сопоставлении групп агрессивных (nf =10) и неагрессивных юношей (п2=11)

Группы	"Есть эффект": d ≤50			"Нет эффекта". d >50			Суммы
	Количество испытуемых	(% доля)		Количество испытуемых	(% доля)
1 группа -агрессивные юноши		(70%)			(30%)
2 группа -неагрессивные юноши		(180%)			(81,8%)
Сумма

По Табл. XII Приложения 1 определяем величины φ, соответст­вующие процентным долям "эффекта" в каждой из групп.

Полученное эмпирическое значение φ* находится в зоне значимости.

Ответ: H 0 отвергается. Принимается H 1 . Доля лиц, которые вы­бирают дистанцию в беседе меньшую или равную 50 см, в.группе аг­рессивных юношей больше, чем в группе неагрессивных юношей

На основании полученного результата мы можем сделать заклю­чение, что более агрессивные юноши чаще выбирают расстояние менее полуметра, в то время как неагрессивные юноши чаще выбирают боль­шее, чем полметра, расстояние. Мы видим, что агрессивные юноши общаются фактически на границе интимной (0-46 см) и личной зоны (от 46 см). Мы помним, однако, что интимное расстояние между парт­нерами является прерогативой не только близких добрых отношений, но и рукопашного боя (Hall E . T ., 1959).

Пример 3 - сопоставление выборок и по уровню, и по распреде­лению признака.

В данном варианте использования критерия мы вначале можем проверить, различаются ли группы по уровню какого-либо признака, а затем сравнить распределения признака в двух выборках. Такая задача может быть актуальной при анализе различий в диапазонах или форме распределения оценок, получаемых испытуемыми по какой-либо новой методике.

В исследовании Р. Т. Чиркиной (1995) впервые использовался опросник, направленный на выявление тенденции к вытеснению из па­мяти фактов, имен, намерений и способов действия, обусловленному личными, семейными и профессиональными комплексами. Опросник был создан при участии Е. В. Сидоренко на основании материалов книги 3. Фрейда "Психопатология обыденной жизни". Выборка из 50 студентов Педагогического института, не состоящих в браке, не имею­щих детей, в возрасте от 17 до 20 лет, была обследована с помощью данного опросника, а также методики Менестера-Корзини для выявле­ния интенсивности ощущения собственной недостаточности, или "комплекса неполноценности" (Manaster G . J ., Corsini R . J ., 1982).

Результаты обследования представлены в Табл. 5.4.

Можно ли утверждать, что между показателем энергии вытесне­ния, диагностируемым с помощью опросника, и показателями интенсив­ности, ощущения собственной недостаточности существуют какие-либо значимые соотношения?

Таблица 5.4

Показатели интенсивности ощущения собственной недостаточности в группах студентов с высокой (nj =18) и низкой (п2=24) энергией вытеснения

Группа 1: энергия вытеснения от 19 до 31 балла (n 1 =181		Группа 2: энергия вытеснения от 7 до 13 баллов (n 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Суммы Средние	26,11	15,42

Несмотря на то, что средняя величина в группе с более энергич­ным вытеснением выше, в ней наблюдаются также и 5 нулевых значе­ний. Если сравнить гистограммы распределения оценок в двух выбор­ках, то между ними обнаруживается разительный контраст (Рис. 5.3).

Для сравнения двух распределений мы могли бы применить кри­терий χ 2 или критерий λ , но для этого нам пришлось бы укрупнять разряды, а кроме того, в обеих выборках n <30.

Критерий φ* позволит нам проверить наблюдаемый на графике эффект несовпадения двух распределений, если мы условимся считать, что "эффект есть", если показатель чувства недостаточности принимает либо очень низкие (0), либо, наоборот, очень высокие значения (S 30), и что "эффекта нет", если показатель чувства недостаточности прини­мает средние значения, от 5 до 25.

Сформулируем гипотезы.

H 0 : Крайние значения показателя недостаточности (либо 0, либо 30 и более) в группе с более энергичным вытеснением встречаются не чаще, чем в группе с менее энергичным вытеснением.

H 1 : Крайние значения показателя недостаточности (либо 0, либо 30 и более) в группе с более энергичным вытеснением встречаются ча­ще, чем в группе с менее энергичным вытеснением.

Создадим четырехклеточную таблицу, удобную для дальнейшего расчета критерия φ*.

Таблица 5.5

Четырехклеточная таблица для расчета критерия φ*при сопоставлении групп с большей и меньшей энергией вытеснения по соотношению пока­зателей недостаточности

Группы	"Есть эффект": показатель недостаточности равен 0 или >30		"Нет эффекта": показатель недос­таточности от 5 до 25		Суммы
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Суммы

По Табл. XII Приложения 1 определим величины ф, соответст­вующие сопоставляемым процентным долям:

Подсчитаем эмпирическое значение φ*:

Критические значения φ* при любых n 1 , n 2 , как мы помним из предыдущего примера, составляют:

Табл. XIII Приложения 1 позволяет нам и более точно опреде­лить уровень значимости полученного результата: р<0,001.

Ответ: H 0 отвергается. Принимается H 1 . Крайние значения по­казателя недостаточности (либо 0, либо 30 и более) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энер­гией вытеснения.

Итак, испытуемые с большей- энергией вытеснения могут иметь как очень высокие (30 и более), так и очень низкие (нулевые) показа­тели ощущения собственной недостаточности. Можно предположить, что они вытесняют и свою неудовлетворенность, и потребность в жиз­ненном успехе. Эти предположения нуждаются в дальнейшей проверке.

Полученный результат, независимо от его интерпретации, под­тверждает возможности критерия φ* в оценке различий в форме рас­пределения признака в двух выборках.

В первоначальной выборке было 50 человек, но 8 из них были исключены из рассмотрения как имеющие средний балл по показателю анергии вытеснения (14-15). Показатели интенсивности чувства недостаточности у них тоже средние: 6 значений по 20 баллов и 2 значения по 25 баллов.

В мощных возможностях критерия φ* можно убедиться, под­твердив совершенно иную гипотезу при анализе материалов данного примера. Мы можем доказать, например, что в группе с большей энергией вытеснения показатель недостаточности все же выше, несмот­ря на парадоксальность его распределения в этой группе.

Сформулируем новые гипотезы.

H 0 Наиболее высокие значения показателя недостаточности (30 и бо­лее) в группе с большей энергией вытеснения встречаются не ча­ще, чем в группе с меньшей энергией вытеснения.

H 1 : Наиболее высокие значения показателя недостаточности (30 и бо­лее) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения. Построим четырехпольную таблицу, используя данные Табл. 5.4.

Таблица 5.6

Четырехклеточная таблица для расчета критерия φ* при сопоставлении групп с большей и меньшей энергией вытеснения по уровню показа­теля недостаточности

Группы	"Есть эффект"* показатель недос­таточности больше или равен 30		"Нет эффекта": показатель недостаточности меньше 30		Суммы
1 группа - с большей энергией вытеснения		(61,1%)		(38.9%)
2 группа - с меньшей энергией вытеснения		(25.0%)		(75.0%)
Суммы

По Табл. XIII Приложения 1 определяем, что этот результат соответствует уровню значимости р=0,008.

Ответ: Но отвергается. Принимается Hj : Наиболее высокие показатели недостаточности (30 и более баллов) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энер­гией вытеснения (р=0,008).

Итак, нам удалось доказать и то, что в группе с более энергич­ным вытеснением преобладают крайние значения показателя недоста­точности, и то, что больших своих значений этот показатель достигает именно в этой группе.

Теперь мы могли бы попробовать доказать, что в группе с большей энергией вытеснения чаще встречаются и более низкие значения пока­зателя недостаточности, несмотря на то, что средняя величина в этой группе больше (26,11 против 15,42 в группе с меньшим вытеснением).

Сформулируем гипотезы.

H 0 : Самые низкие показатели недостаточности (нулевые) в группе с большей энергией вытеснения встречаются не чаще, чем в группе с меньшей энергией вытеснения.

H 1 : Самые низкие показатели недостаточности (нулевые) встречаются в группе с большей энергией вытеснения чаще, чем в группе с менее энергичным вытеснением. Сгруппируем данные в новую четырехклеточную таблицу.

Таблица 5.7

Четырехклеточная таблица для сопоставления групп с разной энергией вытеснения по частоте нулевых значений показателя недостаточности

Группы	"Есть эффект": показатель недостаточности равен 0		"Нет эффекта" недостаточности	показатель не равен 0	Суммы
1 группа - с большей энергией вытеснения		(27,8%)		(72,2%)
1 группа - с меньшей энергией вытеснения		(8,3%)		(91,7%)
Суммы

Определяем величины φ и подсчитываем значение φ*:

Ответ: H 0 отвергается. Самые низкие показатели недостаточно­сти (нулевые) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения (р<0,05).

В сумме полученные результаты могут рассматриваться как сви­детельство частичного совпадения понятий комплекса у З.Фрейда и А.Адлера.

Существенно при этом, что между показателем энергии вытесне­ния и показателем интенсивности ощущения собственной недостаточно­сти в целом по выборке получена положительная линейная корреляци­онная связь (р=+0,491, р<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

Пример 4 - использование критерия φ* в сочетании с критерием λ Колмогорова-Смирнова в целях достижения макси­мально точного результата

Если выборки сопоставляются по каким-либо количественно изме­ренным показателям, встает проблема выявления той точки распределе­ния, которая может использоваться как критическая при разделении всех испытуемых на тех, у кого "есть эффект" и тех, у кого "нет эффекта".

В принципе точку, по которой мы разделили бы группу на под­группы, где есть эффект и нет эффекта, можно выбрать достаточно произвольно. Нас может интересовать любой эффект и, следовательно, мы можем разделить обе выборки на две части в любой точке, лишь бы это имело какой-то смысл.

Для того, чтобы максимально повысить мощность критерия φ*, нужно, однако, выбрать точку, в которой различия между двумя сопос­тавляемыми группами являются наибольшими. Точнее всего мы сможем сделать это с помощью алгоритма расчета критерия λ , позволяющего обнаружить точку максимального расхождения между двумя выборками.

Возможность сочетания критериев φ* и λ описана Е.В. Гублером (1978, с. 85-88). Попробуем использовать этот способ в решении сле­дующей задачи.

В совместном исследовании М.А. Курочкина, Е.В. Сидоренко и Ю.А. Чуракова (1992) в Великобритании проводился опрос англий­ских общепрактикующих врачей двух категорий: а) врачи, поддержав­шие медицинскую реформу и уже превратившие свои приемные в фондодержащие организации с собственным бюджетом; б) врачи, чьи при­емные по-прежнему не имеют собственных фондов и целиком обеспечи­ваются государственным бюджетом. Опросники были разосланы вы­борке из 200 врачей, репрезентативной по отношению к генеральной совокупности английских врачей по представленности лиц разного пола, возраста, стажа и места работы - в крупных городах или в провинции.

Ответы на опросник прислали 78 врачей, из них 50 работающих в приемных с фондами и 28 - из приемных без фондов. Каждый из врачей должен был прогнозировать, какова будет доля приемных с фондами в следующем, 1993 году. На данный вопрос ответили только 70 врачей из 78, приславших ответы. Распределение их прогнозов представлено в Табл. 5.8 отдельно для группы врачей с фондами и группы врачей без фондов.

Различаются ли каким-то образом прогнозы врачей с фондами и врачей без фондов?

Таблица 5.8

Распределение прогнозов сбщепрактикующих врачей о том, какова будет доля приемных с фондами в 1993 году

Прогнозируемая доля
приемных с фондами	врачами с фондом (n 1 =45)	врачами без фонда (n 2 =25)	Суммы
1. от 0 до 20%	4	5	9
2. от 21 до 40%	15	И	26
3. от 41 до 60%	18	5	23
4. от 61 до 80%	7	4	И
5. от 81 до 100%	1	0	1
Суммы	45	25	70

Определим точку максимального расхождения между двумя рас­пределениями ответов по Алгоритму 15 из п. 4.3 (см. Табл. 5.9).

Таблица 5.9

Расчет максимальной разности накопленных частостей в распределениях прогнозов врачей двух групп

Прогнозируемая доля приемных с фондами (%)	Эмпирические частоты выбора данной категории ответа		Эмпирические частости		Накопленные эмпи­рические частости		Разность (d)
	врачами с фондом (n 1 =45)	врачами без фонда (n 2 =25)	f* э 1	f* a2	∑f* э1	∑f* а1
1. от 0 до 20% 2. от 21 до 40% 3. от 41 до 60% 4. от 61 до 80% 5. от 81 до 100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

Максимальная выявленная между двумя накопленными эмпириче­скими частостями разность составляет 0,218.

Эта разность оказывается накопленной во второй категории про­гноза. Попробуем использовать верхнюю границу данной категории в качестве критерия для разделения обеих выборок на подгруппу, где "есть эффект" и подгруппу, где "нет эффекта". Будем считать, что "эффект есть", если данный врач прогнозирует от 41 до 100% прием­ных с фондами в 1993 году, и что "эффекта нет", если данный врач прогнозирует от 0 до 40% приемных с фондами в 1993 году. Мы объ­единяем категории прогноза 1 и 2, с одной стороны, и категории про­гноза 3, 4 и 5, с другой. Полученное распределение прогнозов пред­ставлено в Табл. 5.10.

Таблица 5.10

Распределение прогнозов у врачей с фондами и врачей без фондов

Прогнозируемая доля приемных с фондами(%1	Эмпирические частоты выбора данной категории прогноза		Суммы
	врачами с фондом (n 1 =45)	врачами без фонда (n 2 =25)
1. от 0 до 40%	19	16	35
2. от 41 до 100%	26	9	35
Суммы	45	25	70

Полученную таблицу (Табл. 5.10) мы можем использовать, про­веряя разные гипотезы путем сопоставления любых двух ее ячеек. Мы помним, что это так называемая четырехклеточная, или четырехпольная, таблица.

В данном случае нас интересует, действительно ли врачи, уже располагающие фондами, прогнозируют больший размах этого движения в будущем, чем врачи, не располагающие фондами. Поэтому мы услов­но считаем, что "эффект есть", когда прогноз попадает в категорию от 41 до 100%. Для упрощения расчетов нам необходимо теперь повер­нуть таблицу на 90°, вращая ее по направлению часовой стрелки. Можно сделать это даже буквально, повернув книгу вместе с таблицей. Теперь мы можем перейти к рабочей таблице для расчета крите­рия φ* - углового преобразования Фишера.

Таблица 5.11

Четырехклеточная таблица для подсчета критерия φ* Фишера для вы­явления различий в прогнозах двух групп общепрактикующих врачей

Группа	Есть эффект -прогноз от 41 до 100%	Нет эффекта -прогноз от 0 до 40%	Всего
I группа - врачи, взявшие фонд	26 (57.8%)	19 (42.2%)	45
II группа - врачи, не взявшие фонда	9 (36.0%)	16 (64.0%)	25
Всего	35	35	70

Сформулируем гипотезы.

H 0 : Доля лиц, прогнозирующих распространение фондов на 41%-100% всех врачебных приемных, в группе врачей с фондами не больше, чем в группе врачей без фондов.

H 1 : Доля лиц, прогнозирующих распространение фондов на 41%-100% всех приемных, в группе врачей с фондами больше, чем в группе врачей без фондов.

Определяем величины φ 1 и φ 2 по Таблице XII приложения 1. Напомним, что φ 1 - это всегда угол, соответствующий большей про­центной доле.

Теперь определим эмпирическое значение критерия φ*:

По Табл. XIII Приложения 1 определяем, какому уровню значи­мости соответствует эта величина: р=0,039.

По той же таблице Приложения 1 можно определить критические значения критерия φ*:

Ответ: Но отвергается (р=0,039). Доля лиц, прогнозирующих распространение фондов на 41-100 % всех приемных, в группе врачей, взявших фонд, превышает эту долю в группе врачей, не взявших фонда.

Иными словами, врачи, уже работающие в своих приемных на отдельном бюджете, прогнозируют более широкое распространение этой практики в текущем году, чем врачи, пока еще не согласившиеся перей­ти на самостоятельный бюджет. Интерпретации этого результата мно­гозначны. Например, можно предположить, что врачи каждой из групп подсознательно считают свое поведение более типичным. Это может означать также, что врачи, уже перешедшие на самостоятельный бюд­жет, склонны преувеличивать размах этого движения, так как им нужно оправдать свое решение. Выявленные различия могут означать и нечто такое, что вовсе выходит за рамки поставленных в исследовании вопро­сов. Например, что активность врачей, работающих на самостоятельном бюджете, способствует заострению различий в позициях обеих групп. Они проявили большую активность, когда согласились взять фонды, они проявили большую активность, когда взяли на себя труд ответить на почтовый опросник; они проявляют большую активность, когда прогнозируют большую активность других врачей в получении фондов.

Так или иначе, мы можем быть уверены, что выявленный уро­вень статистических различий - максимально возможный для этих ре­альных данных. Мы установили с помощью критерия λ точку макси­мального расхождения между двумя распределениями и именно в этой точке разделили выборки на две части.

Ваша оценка.

Функция ФИШЕР выполняет возвращение преобразования Фишера для аргументов X . Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Используется функция ФИШЕР для того чтобы проверить гипотезу с помощью коэффициента корреляции.

Описание работы функции ФИШЕР в Excel

При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:

• не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
• имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.

Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:

Z"=1/2*ln(1+x)/(1-x)

Рассмотрим применение данной функции на 3-x конкретных примерах.



Оценка взаимосвязи прибыли и затрат по функции ФИШЕР

Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).

Таблица 1 – Исходные данные:

№	X	Y
1	210 000 000,00 ₽	95 000 000,00 ₽
2	1 068 000 000,00 ₽	76 000 000,00 ₽
3	1 005 000 000,00 ₽	78 000 000,00 ₽
4	610 000 000,00 ₽	89 000 000,00 ₽
5	768 000 000,00 ₽	77 000 000,00 ₽
6	799 000 000,00 ₽	85 000 000,00 ₽

Схема решения таких задач выглядит следующим образом:

1. Рассчитывается линейный коэффициент корреляции r xy ;
2. Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение t р > t кр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
3. Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
4. Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
5. Рассчитывается стандартная ошибка линейного коэффициента корреляции.

Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.

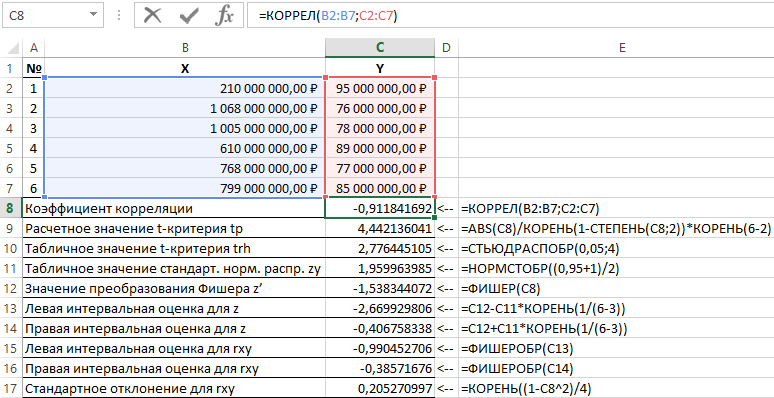
Рисунок 1 – Пример расчетов.

№ п/п	Наименование показателя	Формула расчета
1	Коэффициент корреляции	=КОРРЕЛ(B2:B7;C2:C7)
2	Расчетное значение t-критерия tp	=ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2)
3	Табличное значение t-критерия trh	=СТЬЮДРАСПОБР(0,05;4)
4	Табличное значение стандартного нормального распределения zy	=НОРМСТОБР((0,95+1)/2)
5	Значение преобразования Фишера z’	=ФИШЕР(C8)
6	Левая интервальная оценка для z	=C12-C11*КОРЕНЬ(1/(6-3))
7	Правая интервальная оценка для z	=C12+C11*КОРЕНЬ(1/(6-3))
8	Левая интервальная оценка для rxy	=ФИШЕРОБР(C13)
9	Правая интервальная оценка для rxy	=ФИШЕРОБР(C14)
10	Стандартное отклонение для rxy	=КОРЕНЬ((1-C8^2)/4)

Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.

Проверка статистической значимости регрессии по функции FРАСПОБР

Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.

Для проверки значимости уравнения в целом выдвинем гипотезу Н 0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н 1 о статистической значимости коэффициента детерминации:

Н 1: R 2 ≠ 0.

Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.

Таблица 2 – Исходные данные

Для этого используем в пакете Excel функцию:

FРАСПОБР (α;p;n-p-1)

• α – вероятность, связанная с данным распределением;
• p и n – числитель и знаменатель степеней свободы, соответственно.

Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для F крит (см. рисунок 2).

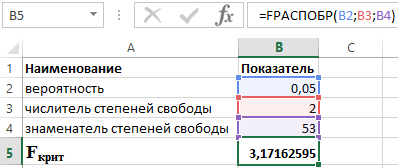
Рисунок 2 – Пример расчетов.

Таким образом можно сказать, что F расч > F крит. В итоге принимается гипотеза Н 1 о статистической значимости коэффициента детерминации.

Расчет величины показателя корреляции в Excel

Пример 3. Используя данные 23 предприятий о: X - цена на товар А, тыс. руб.; Y - прибыль торгового предприятия, млн. руб, производится изучение их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве модели регрессии.

Определим F крит из выражения:

F расч = R 2 /23*(1-R 2)

где R – коэффициент детерминации, равный 0,67.

Таким образом, расчетное значение F расч = 46.

Для определения F крит используем распределение Фишера (см. рисунок 3).

Рисунок 3 – Пример расчетов.

Таким образом, полученная оценка уравнения регрессии надежна.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью -критерия Фишера:

, (2.22)

где
– факторная сумма квадратов на одну степень свободы;
– остаточная сумма квадратов на одну степень свободы;
– коэффициент (индекс) множественной детерминации;
– число параметров при переменных(в линейной регрессии совпадает с числом включенных в модель факторов); – число наблюдений.

Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный
-критерий, т.е..

Частный
-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для факторачастный
-критерий определится как

, (2.23)

где
– коэффициент множественной детерминации для модели с полным набором факторов,
– тот же показатель, но без включения в модель фактора,– число наблюдений,
– число параметров в модели (без свободного члена).

Фактическое значение частного
-критерия сравнивается с табличным при уровне значимости
и числе степеней свободы: 1 и
. Если фактическое значение превышает
, то дополнительное включение факторав модель статистически оправданно и коэффициент чистой регрессиипри факторестатистически значим. Если же фактическое значениеменьше табличного, то дополнительное включение в модель факторане увеличивает существенно долю объясненной вариации признака, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

Для двухфакторного уравнения частные
-критерии имеют вид:

,
. (2.23а)

С помощью частного
-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий факторвводился в уравнение множественной регрессии последним.

-Критерий стьюдента для уравнения множественной регрессии.

Частный
-критерий оценивает значимость коэффициентов чистой регрессии. Зная величину, можно определить и-критерий для коэффициента регрессии при-м факторе,, а именно:

. (2.24)

Оценка значимости коэффициентов чистой регрессии по -критерию Стьюдента может быть проведена и без расчета частных
-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула:

, (2.25)

где – коэффициент чистой регрессии при факторе,– средняя квадратическая (стандартная) ошибка коэффициента регрессии.

Для уравнения множественной регрессии средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:

, (2.26)

где ,– среднее квадратическое отклонение для признака,
– коэффициент детерминации для уравнения множественной регрессии,
– коэффициент детерминации для зависимости факторасо всеми другими факторами уравнения множественной регрессии;
– число степеней свободы для остаточной суммы квадратов отклонений.

Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации
. Так, для уравнения
оценка значимости коэффициентов регрессии,,предполагает расчет трех межфакторных коэффициентов детерминации:
,
,
.

Взаимосвязь показателей частного коэффициента корреляции, частного
-критерия и-критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинами. Частный
-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.